HNUST-计算机图形/图像期末复习-1.9 21:40更新
ZealSinger 发布于 阅读:18579 期末复习
最后加入了“猜题大王模块”,有想法在评论区可以一起猜题,已开启评论区
教材
考试题型(源自CSDN)
-
简述题(10分×4题,共40分)
-
第1章的基本内容
-
三维观察流水线中的基本概念与理解
-
三维场景真实感绘制中的基本概念与理解
-
图像增强中的基本概念与理解
-
形态学操作,包括膨胀,腐蚀,开,闭等操作中的基本概念与理解
-
-
计算题(共10分)
-
Bézier样条的计算表达
-
-
编程题(共30分)
-
OpenCV基本函数的调用
-
利用OpenGL编写核心代码,包括平移,旋转,缩放及坐标系之间的变换等所有其它的基本变换。
-
利用OpenCV编写核心代码,内容包括图像增强,图像分析等
-
-
问答题(共20分 老师没讲)
第一章和第十章内容,考得宽泛,无需写具体知识点,但回答尽量多写字数,预估送分题,例如:
计算机图形学和数字图像处理这两门学科的关系 图像处理有哪些细分领域与自己有什么关系
对比学校PDF,整体结构式一样的,但是分值分配不一样,计算题比例会更多一点,很明显这样子难度更大

第一章:计算机图形学概述
相关定义
计算机图像学定义
研究怎么利用计算机表示,生成,处理和显示图形的原理,算法,方法和技术的一门学科,计算机图形学=造型+绘制
图形的构成要素
图形由 几何要素 和 非集合要素 两种要素构成
-
几何要素:刻画形状的点,线,面,体等
-
非几何要素:反映物体表面属性和材质的灰度,颜色等
例如: 方程x+y=1确定的图形由满足这个方程并且具有一定颜色信息的点构成 (几何要素:满足x+y=1的点 非几何要素:具有一定的颜色信息)
图形的表示方法
一般有 参数法 和 点阵法 两种表示图形的方法
-
参数法:用图形的形状参数 和 属性参数 来表示图形,用参数法描述的图形叫做参数图或者图形
-
形状参数:是指描述图形的方程;分析表达式的系数;线段的端点坐标;多边形的顶点坐标等
-
属性参数:包括颜色和线性
-
-
点阵法:通过列出图形中所有的点来表示图形,用点阵法描述的图形叫做像素图或者图像。点阵法强调的是“图形由哪些点组成,每个点具有怎样的颜色”
计算机图形学的研究内容
-
图形的输入:开发和利用图形输入设备以及相关软件把图形输入到计算机中,以便于进行各种处理
-
图形的处理:对图形进行变换(例如几何变换,投影变换 )和运算(例如图形的交,并,差运算)等处理
-
图形的生成和输出:将图形的特定表示形式转换为图形输出系统便于接受的表示形式,并将图形在显示器或者打印机等输出设备上输出
计算机图形学与相关学科的关系
主要探讨计算机图形学,图形处理,计算机几何,计算机视觉和模式识别这几个学科之间的关系,一张图

计算机图形学的应用领域
-
计算机辅助设计(CAD)与制造 (这个是计算机图形学在工业界最成功,最重要的领域)
-
科学计算可视化
-
虚拟现实(VR)
-
计算机艺术
-
计算机动画(CG)
-
图形用户接口(GUI)
第二章:基本图元的显示
万万没想到这个地方就会有计算题,帧缓冲器的相关内容
帧缓冲器的定义
图形的定义保存在称之为刷新缓冲器/帧缓冲器的存储器中。该存储器保存屏幕上所有位置的强度值,每次考试刷新时,从刷新缓冲区中取出强度值并在屏幕上画出。
对应计算题P18习题5
分辨率1024x768,代表一共能存放多少个像素
32位系统,代表一个像素需要用32位表示
那么总共就需要
1024*768*32=25165824 位
因为题目问的是多少MB,所以要进行单位转换
25165824/8/(1024*1024) = 3MB
DDA画线算法
对于两点确认的一条直线,我们假设其满足y=kx+b,假设两个端点现在分别是(x1,y1)和(x2,y2)
我们选择一个主方向(变化较大的一方),主方向增加一个单位,假设我们选择x方向为主方向,那么y方向我们称之为从方向
则下一步点的位置(x1+ 1,y1+1)则需要满足 y1+1=k(x1 + 1)+ b,那么得到了 y1+1 = y1+k
也就是说,主方向每增加一个单位,从方向对应的增加k
直接看题(教材P13):使用DDA算法绘制端点为(20, 10)和(28, 16)的线段
x1=20,x2=28,x2-x1=8
y1=10.y2=16,y2-y1=6
x的差值更大,x变化更大,所以x为主方向
求得k=6/8=0.75
x1=20,y=10
x2=20+1=21,y2=10+k=10.75=11
// 注意 坐标数据是四舍五入之后的 但是计算过程中使用的是真实结果值
x3=21+1=22,y3=10.75+k=11.5=12
x4=23,y4=11.5+k=12.25=12
(按需看代码,不确定会不会考)

第三章:OpenGL
OpenGL基础(编程题理论基础)
本部分是关于OpenGL的相关内容介绍,涉及到了很多标准库函数,可以有个大致的概念和印象,本部分笔记内容也没有全部将书上的内容都写入,因为不太清楚考的多有哪些,在后续的习题中可以返回来再看看,做题后才能知道哪些是重点考的函数,然后再统一记忆。
OpenGL(Open Graphics Library)的核心目标是渲染图形,即根据几何数据(点、线、面)和非几何数据(颜色、材质、纹理),在屏幕上绘制出 2D 或 3D 图像。它是一个底层的图形 API,提供了操作图形硬件的接口。专注于图形渲染,将几何数据转换为屏幕上的像素
了解定义是为了能和OpenCV的作用进行区分,方便理解而已,应该不存在考点的说法
基础语法
学习常规基础语法之前,先来聊聊OpenGL整个库的组成部分,个人认为是有助于了解命名规范和记忆函数作用
基于三大组成部分的命名规范
-
gl: 核心函数,直接与图形硬件交互,如
glClearColor,glVertex3f。 -
glu: 实用函数库(OpenGL Utility Library),封装了一些常用操作,如
gluOrtho2D(正交投影)、gluPerspective(透视投影)。 -
glut: 实用工具包(OpenGL Utility Toolkit),用于窗口管理、事件处理、简单的 3D 模型绘制,如
glutInit,glutCreateWindow,glutDisplayFunc。
三大组成部分决定了函数的前缀,也决定了函数放在哪里,同时对于函数的作用也有一定的提示性。例如你看到glxxxx函数就立马能反应属于核心函数且与图形硬件交互有关
同时,基于三大组成部分,每个组成部分内肯定会定义一些常量,这些常量的命名也是和所属部分相关
-
GL_: 核心常量,如
GL_COLOR_BUFFER_BIT,GL_LINE_LOOP。 -
GLU_: 实用库常量。
-
GLUT_: 工具包常量,如
GLUT_RGB,GLUT_DOUBLE。
OpenGL的函数后缀的设计也是有一定规范的,你可以看到很多函数名都是类似的3f,3fv,2d这种数字+字母的形式为函数名的后缀
-
数字:表示参数个数,如
glVertex2f(2 个参数)、glVertex3f(3 个参数)。 -
字母:表示参数类型,如
f(float)、d(double)、i(int)、v(vector,向量)。示例:
-
glVertex3f(1.0f, 0.0f, 0.0f):3 个 float 参数,表示一个 3D 点。 -
glColor3fv(colors):一个包含三个元素的 float 向量(数组),表示 RGB 颜色。
-
当然,也存在一部分特殊的命名,例如GLint, GLfloat, GLdouble, GLubyte 等,确保跨平台兼容性。
程序基本框架(重要)
所有OpenGL相关的程序题的基础架构,哪怕这个题目不会写,也可以先把这个整体架构写上去,类似于高考公式分
如下代码,是运行一个最基本的OpenGL所需要的代码(教材P5),其运行后的效果是
一个 200×200 的窗口,标题是「First OpenGL!」:
-
背景是默认的黑色;
-
窗口中间会显示一个白色矩形(因为
glColor默认是白色(1,1,1,1)),矩形的范围是(-0.8,-0.6)到(0.8,0.6)(对应 OpenGL 默认的「标准化设备坐标」,范围是[-1,1])。
void Paint() // 对象的描述
{
glClear(GL_COLOR_BUFFER_BIT); // 清除颜色缓冲区 GL_COLOR_BUFFER_BIT即代表颜色缓冲区
glRectf(-0.8,-0.6,0.8,0.6); // 定义矩形 (-0.8,-0.6)~(0.8,0.6) 语法糖 封装了待会儿下面要说的 glBegin(GL_QUADS)操作
glFlush(); // 强制 OpenGL 命令序列在有限的时间内完成执行 也代表绘图的结束
}
int main(int argc,char *argv[])
{
// 初始化 GLUT,记录 main()的参数,理解不了的直接死记硬背,入参就是main函数的入参,只不过第一个argc参数需要取地址
glutInit(&argc,argv);
// 设置程序窗口的显示模式(GLUT_SINGLE表示设置为单缓存,GLUT_RGBA表示设置为RGBA颜色模式,除此之外还有GLUT_INDEX索引颜色模型,CLUT_DOUBLE双线是缓冲区,GLUT_DEPTH深度缓存),glutInitDisplayMode的默认模式是GLUT_SINGLE | GLUT_RGBA即RGBA颜色方式的单缓冲区,也就是说即使你不设置,默认也是GLUT_SINGLE | GLUT_RGBA
// 需要注意的是 RGBA的颜色参数其实有四个(red,green,blue,alpha)前三个即代表红绿蓝的占比,最后一个alpha代表透明度,默认为1,代表完全不透明,四个参数的取值都是[0,1]
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGBA);
glutInitWindowSize(200,200); // 初始化窗口位置。指定程序窗口在屏幕上的大小
glutCreateWindow("First OpenGL!"); // 创建程序窗口,指定窗口标题
glutDisplayFunc(Paint); // 指定场景绘制循环函数,必需
glutMainLoop(); // 开始循环执行 OpenGL 命令
}基本图元绘制
常见图元类型,对应教材P26
-
GL_POINTS:点
-
GL_LINES:线段(每两个顶点组成一条)
-
GL_LINE_STRIP:折线(顶点依次相连)
-
GL_LINE_LOOP:闭合折线
-
GL_TRIANGLES:三角形(每三个顶点一个)
-
GL_TRIANGLE_STRPI:三角形带
-
GL_TRIANGLE_FAN:三角形扇
-
GL_QUADS:四边形
-
GL_POLYGON:多边形
当你需要某种图元类型的绘画的时候,统一采用如下的格式/框架
glBegin(图元类型);
相关参数
glEnd();
例如
// 绘制 4 个独立的点,分别位于坐标 (-1,1)、(1,1)、(1,-1)、(-1,-1) 处
glBegin(GL_POINTS); // 绘点
// glVertex2f按照我们上面的命名规范可以拆分理解
// gl(核心库函数)+Vertex(英文翻译为顶点)+2f(代表接收两个float类型的参数)
// 所以综合理解就是 核心库函数中的 利用两个float入参 可以绘画一个顶点 的方法
glVertex2f(-1, 1); // 左上点
glVertex2f(1, 1); // 右上点
glVertex2f(1, -1); // 右下点
glVertex2f(-1, -1); // 左下点
glEnd();
// 每两个顶点组成一条线段,这里将绘制两条交叉的线段,形成一个 "X" 形,一条连接 (-2,2) 到 (2,-2),另一条连接 (-2,-2) 到 (2,2)。
glBegin(GL_LINES); // 线段
// 第一条线段
glVertex2f(-2, 2);
glVertex2f(2, -2);
// 第二条线段
glVertex2f(-2, -2);
glVertex2f(2, 2);
glEnd();
//顶点依次连接形成连续的折线,从 (-2,0) 到 (0,2),再到 (2,0),最后到 (0,-2),形成一个不闭合的菱形轮廓。
glBegin(GL_LINE_STRIP); //折线(顶点依次相连)
glVertex2f(-2, 0);
glVertex2f(0, 2);
glVertex2f(2, 0);
glVertex2f(0, -2);
glEnd();
// 顶点依次连接形成折线,并且最后一个顶点会与第一个顶点连接形成闭合图形,这里将形成一个五边形轮廓
glBegin(GL_LINE_LOOP); // 闭合折线
glVertex2f(-2, 1);
glVertex2f(0, 2);
glVertex2f(2, 1);
glVertex2f(1, -1);
glVertex2f(-1, -1);
glEnd();
// 每三个顶点组成一个独立的三角形,这里将绘制两个三角形,它们共享一个顶点 (0,2),形成一个类似蝴蝶翅膀的形状
glBegin(GL_TRIANGLES); // 三角形
// 第一个三角形
glVertex2f(-2, 1);
glVertex2f(0, 2);
glVertex2f(-1, -1);
// 第二个三角形
glVertex2f(0, 2);
glVertex2f(2, 1);
glVertex2f(1, -1);
glEnd();
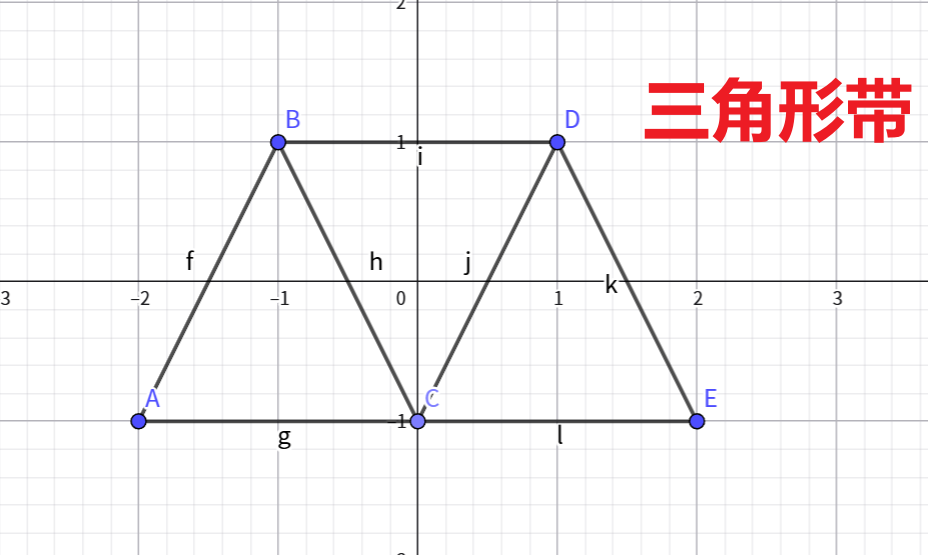
//从第一个顶点开始,每新增一个顶点就与前两个顶点组成一个新三角形,形成连续相连的三角形带,这里会形成一个波浪状的条带图形。
glBegin(GL_TRIANGLE_STRIP); //三角形带 下面有对应的图
glVertex2f(-2, -1);
glVertex2f(-1, 1);
glVertex2f(0, -1);
glVertex2f(1, 1);
glVertex2f(2, -1);
glEnd();
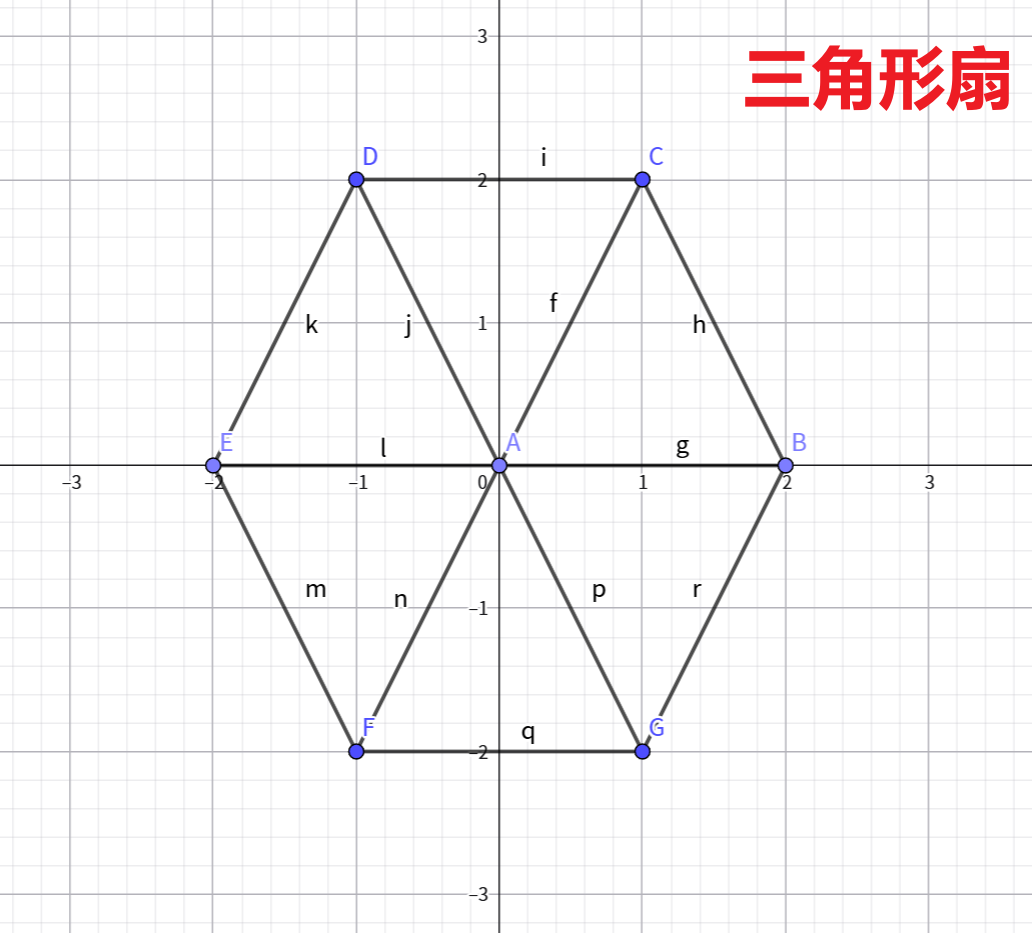
// 以第一个顶点为中心,后续每个顶点与前一个顶点及中心点组成三角形,形成类似扇形的形状,这里会形成一个六边形。
glBegin(GL_TRIANGLE_FAN); // 三角形扇 下面有对应的图
glVertex2f(0, 0); // 中心点
glVertex2f(2, 0);
glVertex2f(1, 2);
glVertex2f(-1, 2);
glVertex2f(-2, 0);
glVertex2f(-1, -2);
glVertex2f(1, -2);
glVertex2f(2, 0); // 闭合图形
glEnd();
// 所有顶点依次连接形成一个闭合的多边形,这里将绘制一个六边形,顶点按顺时针方向排列形成规则的六边形形状。
glBegin(GL_POLYGON);
glVertex2f(-1, 2);
glVertex2f(1, 2);
glVertex2f(2, 0);
glVertex2f(1, -2);
glVertex2f(-1, -2);
glVertex2f(-2, 0);
glEnd();
在书本的P26-3.3.4部分,介绍了一些OpenGL的预定义好的几何图形,也就是内置了一些写好的图形,可以不需要我们自己去绘制,如果觉得需要可以自己记忆背诵这些预定义的函数原型
基本图元属性
这一块是对上面的基本图元的属性的相关设置的函数介绍,对应教材P30-34,但是因为扫了一圈感觉实际考试中这些函数用的很少,故暂且不做介绍,遇到了再说
颜色与材质的设置
-
设置颜色:
glColor3f(r, g, b)(RGB)或glColor4f(r, g, b, a)(RGBA,a 为透明度)。 -
材质属性:3D 绘图中使用,如
glMaterialfv设置材质的漫反射、镜面反射等属性。
第四章和第五章:图形变换
第四章和第五章的内容是一起的,第四章的内容是第五章的铺垫,一起看了
几何变换理论基础
二维图像和三维图像的三种基本变换都是:平移,绕坐标轴旋转/旋转和缩放(P38,57)
-
平移:
glTranslatef(x, y, z)和glTranslated(x,y,z)两个函数的区别在于精度,第一个以
f结尾,代表三个参数都是float类型;第二个则说明参数精度为double,三个参数分别代表沿着X轴(正数代表向右,负数代表向左),Y轴+ 上 /- 下),Z轴(+ 近 /- 远)移动多少,仅改变位置,不改变大小 / 朝向 -
旋转:
glRotatef(angle, x, y, z) 和 glRotated(angle, x, y, z)angle 为
角度,单位为度°,(x,y,z):旋转轴方向向量(x 轴→(1,0,0)、y 轴→(0,1,0)、z 轴→(0,0,1)) -
缩放:
glScalef(x, y, z) 和 glScaled(x, y, z)xyz代表缩放比例,如果大于1则效果为放大,小于1但大于0则是缩小。以原点为中心缩放,比例为负时会镜像翻转
三维复合变换
现实中和题目中,更多的是旋转和反射这些非基本变换,但是实际上所有的非基本变换都是由基本变化复合而来,通过将复合操作拆分为基本操作,就能很好的理解和解答
通用三维旋转(绕某个直线进行旋转)
-
已知:两个点
P0(x0,y0,z0)和P1(x1,y1,z1)(这两个点确定了一条直线,就是我们要绕的 “旋转轴”),旋转轴为P0P1,旋转角度为θ -
目标:让已知物体绕
P0P1这条直线旋转θ角度 -
核心思路
-
把旋转轴
P0P1平移,让其能经过坐标原点 -
把平移后经过原点的
P0P1进行旋转,保证其和某个坐标轴重合(假设我们选择Z轴) -
绕
Z轴(第二步骤中与哪一条坐标轴重合,这里就绕哪一条坐标轴)旋转目标旋转角度θ -
把旋转轴
P0P1转回原来的方向(撤销操作2) -
把旋转轴
P0P1平移回原来的位置(撤销操作1)
-
-
程序代码
// 步骤5:使旋转轴回到原来的位置(把P0点移回原位)
glTranslated(x0, y0, z0);
// 步骤4:使旋转轴回到原来的方向(撤销步骤2的方向调整)
glMultMatrixd((const double[]){
u1, u2, u3, 0,
v1, v2, v3, 0,
n1, n2, n3, 0,
0, 0, 0, 1
});
// 步骤3:绕坐标轴(z轴)完成指定旋转(转θ度)
glRotated(th, 0, 0, 1);
// 步骤2:使旋转轴与某坐标轴(比如z轴)重合(调整方向)
glMultMatrixd((const double[]){
u1, v1, n1, 0,
u2, v2, n2, 0,
u3, v3, n3, 0,
0, 0, 0, 1
});
// 步骤1:使旋转轴通过坐标原点(把P0点移到原点)
glTranslated(-x0, -y0, -z0); -
补充
上述代码涉及到了一些底层和书本上的数学基础需要,秉持着非必要不学数学的理念,我们这里可以强行记忆即可。
步骤一其实是因为
glRotatef/glRotated底层是只能绕 “经过坐标原点 (0,0,0)” 的轴旋转步骤二这个地方涉及到了旋转的相关内容,需要知道旋转的函数为
glMultMatrixd((const double[]),至于旋转操作和逆操作(步骤四),先纯记忆,注意步骤二和步骤四的函数的入参数组不一样哈保证步骤三和对应的旋转轴一样
通用反射轴反射
所谓的反射,其实就是我们常说的对称
-
已知:已知反射轴为P0P1,P0={x0,y0,z0},P1={x1,y1,z1}
-
目标:求已知物体以
P0P1这条直线为对称轴进行对称 -
核心思路
-
平移:把反射轴 P0P1 移到过坐标原点(让 P0 点到原点);
-
旋转:把过原点的反射轴旋转到与 X 轴完全重合(这里也是任意坐标轴重合即可,这里演示为X轴)
-
反射:执行 OpenGL 直接支持的 “绕 X 轴反射”(Y/Z 坐标取反,X 不变);
-
逆旋转:把坐标系转回反射轴原来的方向;
-
逆平移:把反射轴移回原始位置。
-
-
程序代码
glTranslated(x0, y0, z0); // (5) 使反射轴回到原来的位置
glMultMatrixd((const double[]){ // (4) 使反射轴回到原来的方向
u1, u2, u3, 0,
v1, v2, v3, 0,
n1, n2, n3, 0,
0, 0, 0, 1
});
glScaled(1, -1, -1); // (3) 关于坐标轴完成指定的反射(关于X轴反射)
glMultMatrixd((const double[]){ // (2) 使反射轴与某坐标轴重合(X轴)
u1, v1, n1, 0,
u2, v2, n2, 0,
u3, v3, n3, 0,
0, 0, 0, 1
});
glTranslated(-x0, -y0, -z0); // (1) 使反射轴通过坐标原点
通用反射面反射
-
已知:反射面的方程为ax+by+cz+d=0 ,且点(x0,y0,z0)在反射面上
-
目标:求该反射变换的变换矩阵
-
核心思路:要对 “过 (x0,y0,z0)、法向量为 (a,b,c)” 的平面做反射,本质是 5 步变换
-
平移:把反射面的中心点 (x0,y0,z0) 移到坐标原点(让反射面过原点);
-
旋转:把反射面旋转到和 XY 平面重合(也可以是别的平面,例如XZ,YZ);
-
简单反射:对 XY 平面(与上一步一致)做反射,如果是XY平面反射那么就是Z 坐标取反;
-
逆旋转:把坐标系旋转回原来的方向;
-
逆平移:把坐标系平移回原来的位置。
-
-
程序代码
glTranslated(x0, y0, z0); // (5) 使反射面回到原来的位置
glMultMatrixd((const double[]){ // (4) 使反射面回到原来的方向
u1, u2, u3, 0,
v1, v2, v3, 0,
n1, n2, n3, 0,
0, 0, 0, 1
});
glScaled(1, 1, -1); // (3) 关于坐标平面完成指定的反射(XY平面)
glMultMatrixd((const double[]){ // (2) 使反射面与某坐标平面重合(XY平面)
u1, v1, n1, 0,
u2, v2, n2, 0,
u3, v3, n3, 0,
0, 0, 0, 1
});
glTranslated(-x0, -y0, -z0); // (1) 使反射面通过坐标原点
按照PPT,第五章的重点就是上面那些,剩余的内容暂时先不看了
三维观察流水线
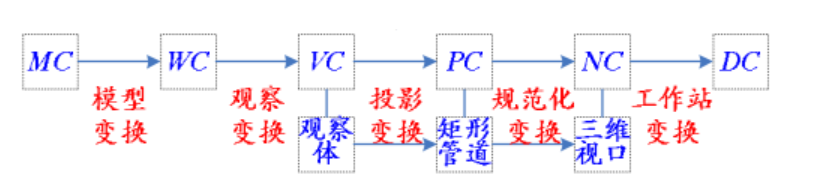
模型变换
迷迷糊糊的,不知道怎么考,简要带过
概念
从模型坐标系到世界坐标系的变换。
3D建模之初,模型有自己的坐标系,以及相应的点坐标。如果放到一个世界坐标系中,需要将它自身的坐标点全部移动到给定位置。
方法
首先构造从世界坐标系到模型坐标系的变换,然后计算该变换的逆变换。(M = (RT)-1 = T-1R-1)
-
使模型坐标系的原点与世界坐标系的原点重合
-
使模型坐标系的坐标轴与世界坐标系的坐标轴重合
-
计算上述2个变换复合以后的逆变换。
投影
所谓投影就是:观察坐标系→投影坐标系,将三维场景投影到二维平面上。
分为平行投影和透视投影,平行投影细分为正投影和斜投影
第六章和第七章
按照CSDN上来看,第六章不重要第七章重要;按照PPT上来看,第六章重要第七章不重要....无语了.....依旧先水一水
顶点变化步骤
(1)指定视图和造型变换。
(2)指定投影变换。
(3)指定视口变换。
模型坐标 →(经过视图造型变换)→ 观察坐标 →(经过投影变换)→ 规范化坐标 →(经过视口变换)→ 窗口坐标

第八章(记概念即可应该,无程序)
OpenGL 的光是由红、绿、蓝组成的。光源的颜色由其所发出的红绿蓝颜色的数量决定,材料的属性用反射的红绿蓝颜色的百分比表示。
光源的构成:
光源由环境光成分(简称为泛光)、漫反射成分和镜面反射成分三部分构成。
-
环境光成分。来自环境,在各方向均匀分布。
-
漫反射成分。来自某一特定方向,一旦照射到表面上,无论在何处观察,亮度都相同。
-
镜面反射成分。来自某一特定方向,以一特定方向离开。
材料颜色:
-
取决于材料对红绿蓝光的反射能力,包括环境光反射(简称为泛射)、漫反射和镜面反射。
-
材料的环境光反射与光源的环境光成分相对应。
-
材料的漫反射与光源的漫反射成分相对应。
-
材料的镜面反射与光源的镜面反射成分相对应。
-
材料的环境光反射和漫反射定义材料的颜色,两者通常是相似的,镜面反射通常是白或灰。
第九章:样条方法(计算题,重点,貌似年年考)
理论知识贼难,但是主要还是看Bézier曲线,所以最好直接略过数学理论基础,能直接看懂Bézier
Bézier基函数

Bézier曲线
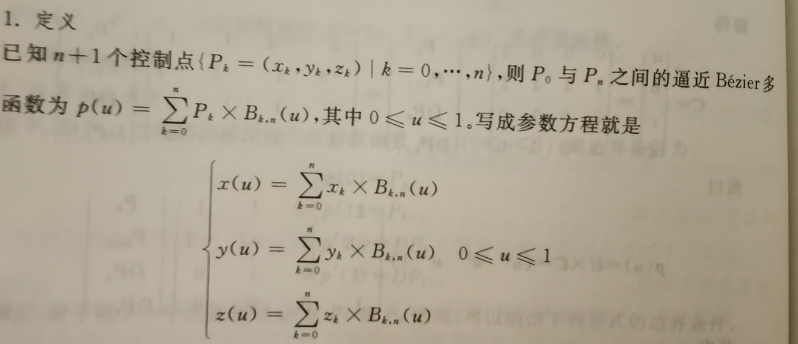
三次Bézier曲线(P126-127)
三次Bézier曲线是最常用的Bézier曲线之一,按照上面的定义,其实就是一共了3+1个控制点的 Bézier 曲线
那么对应的表达式就是
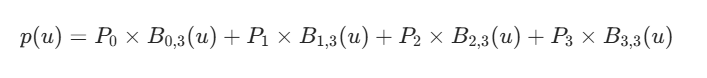
再根据Bézier基函数可以得到

将上述两式子转化为矩阵形式,即为如下

其中M(Bez)称之为三次Bézier样线的基本矩阵,M(geom)就是控制点组成的矩阵
用U依次乘上M(Bez)的每一行和M(geom)的对应行最后相加,就可以得到前面的表达式
(u^3 u^2 u 1) (-1 3 -3 1) p0 + (u^3 u^2 u 1) (3 -6 3 0) p1 ... = p(u)
聪明的大学生看不懂脑残的公式,有了大致的概念,下面直接做例题进行巩固
例题
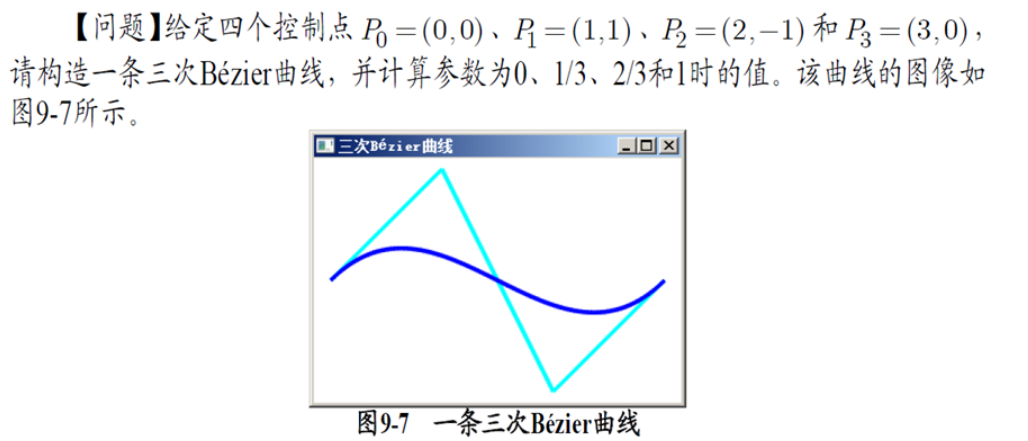
-
分析:已知了四个控制点P0-P3,需要我们求得是参数为0,1/3,2/3和1的时候的值,整个三次Bézier曲线的基函数即p(u),那我们的目标就是求出p(u)的表达式然后分别计算p(0),p(1/3),p(2/3),p(1)即可
-
解答:
根据p(u)的矩阵形式

因为都是三次,U和M(Bez)是一样的,M(geom)根据题目给的坐标点带入即可,那么我们可以先计算M(Bez) * M(geom)
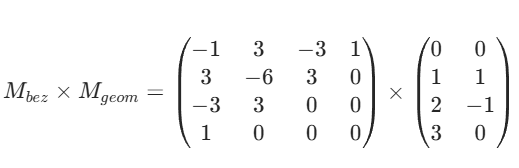
得到结果为
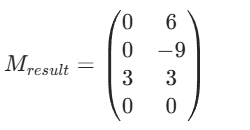
然后再让M(result)和U相乘
用 U=(u^3,u^2,u,1) 分别乘 M(result) 的 第一列、第二列,得到曲线的(x,y)坐标,最后得到
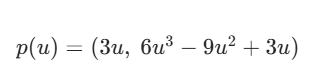
此时,我们就可以代入题目中要求的几个点进行计算得到结果

第十章开始其实就是另外一门课的内容,这本书本身就是二合一,前面是计算机图形学,第十章开始就是数字图像处理
第十章:数字图像处理概述(概念记忆)
-
图像的含义:图像这个词包含的内容很广,凡是记录在纸上,拍摄在照片上,显示在屏幕上的所有具有视觉效果的画面都可以称之为图像
-
图像的分类
-
模拟图像
-
数字图像
-
-
数字图像处理:利用数字计算机以及其他有关的数字技术,对数字图像进行某种运算和处理,使得图像中的某部分信息更加突出,以适应某种特殊需求,达到某种预期目的
-
基本的数字图像处理技术:若无特别说明,基本都是指使用计算机的数字图像处理,包括图像数据格式,图像变换,图像解析和图像数据压缩等
-
数字图像处理的研究内容:图像的数字化;图像的增强;图像恢复;图像编码;图像分析
-
图像处理的主要应用领域:
-
宇宙探索:图像处理的最先应用领域,主要用于地外星体图像的获取,传送和处理
-
通信领域:可视电话,会议电视,多媒体通信等等
-
遥感技术:航空遥感和卫星遥感,主要用于地形和资源的勘测
-
生物医学:X射线,超声,显微图像分析
-
军事:导弹的精准制导,侦察照片的判读,模拟训练等
-
公安:指纹识别,人脸识别,不完整图像的复原等
-
天气预报:天气云图的绘制和传输,卫星云图的处理和试别等
-
考古:文物的辅助恢复
-
-
图像处理与计算机图形学的区别:PPT上有说到但是书上好像没找到对应的内容,以下内容来自AI
图像处理是 “图像→图像 / 分析结果,加工现有图像,不会产生新图像;图形学是 “模型→图像”,会创造新图像。
第十一章:OpenCV(考点主要体现在程序题,不太会出现单独的章节内容出题)
猜测主要考的应该是Open CV GUI命令,对应P159的11.1
-
void namedWindow(const string &name)-
创建一个可以放图片和滑块的窗口
-
参数
name是窗口的名字,可以用于区分窗口和引用窗口并且显示窗口标题 -
如果已经存在
name的窗口,则该函数不会进行任何操作
-
-
void imshow(const string &name, InputArray image);-
在指定为
name的窗口中展示图片image -
黑白的和彩色的图片都可以显示
-
OpenCV中的彩色图片是BGR顺序,不是RGB
-
-
Mat imread(const String &filename, int flags=IMREAD_COLOR);-
从指定文件
filename读取图片,flags参数标识读取图片的方式,默认为IMREAD_COLOR读取成彩色图,对应1,除此之外还可以为IMREAD_GRAYSCALE读取成黑白图,对应0;IMREAD_UNCHANGED不转换载入图像,对应-1 -
如果文件路径错误或者不存在,范围值
Mat会为空
-
-
bool imwrite(const string &filename, InputArray image)-
将
image存入到本地文件filename中 -
只能存 “单通道(黑白)” 或 “3 通道 BGR 顺序” 的图片,否则要先转换格式
-
-
int waitKey(int delay=0);-
等待键盘事件,
delay代表等待毫秒数,0代表无线等待,该函数返回按键对应的数字
using namespace cv;
using namespace std;
int main()
{
// 1. 读图片到Mat里
Mat im = imread("Flower.bmp");
// 2. 检查是否读成功,失败就退出
if(im.empty()) return -1;
// 3. 在叫“WaitKey”的窗口里显示图片
imshow("WaitKey", im);
// 4. 等按键,按Esc(返回27)就退出;按其他键执行对应的操作
for(int c=waitKey(); c!=27; c=waitKey())
{
switch(toupper(c)) // 把按键转成大写
{
case 'X': cout<<"X pressed\n"; break; // 按X,输出提示
case 'Y': cout<<"Y pressed\n"; break; // 按Y,输出提示
case 'S': imwrite("Flower.png", im); break; // 按S,存图片
}
}
}
-
-
typedef void (*MouseCallback)(int event, int x, int y, int flags, void *userdata)-
定义一个鼠标事件响应/回调函数
-
event为鼠标动作,包括但不限于鼠标移动,数标左键按下,右键按下,左键抬起等等 -
(x,y)代表发生鼠标事件的时候,光标在图片上的坐标系位置,以图像左上角为原点,注意不是针对于整个桌面
-
flags标记是否有同时按下ctrl/shift键 -
userdata传递给回调函数的额外信息,自定义
-
-
void setMouseCallback(const string &winname, MouseCallback onMouse, void *userdata=0);-
将回调函数注册到对应的窗口上
-
winname为要注册的窗口 -
onMouse回调函数,也就是上一个函数的返回值 -
userdata传递给回调函数的额外信息,自定义
using namespace cv;
using namespace std;
// 定义鼠标动了要执行的函数(回调函数)
void on_mouse(int event, int x, int y, int flags, void *param)
{
if(event==EVENT_LBUTTONDOWN) // 如果左键按下
{
if(flags & EVENT_FLAG_CTRLKEY) // 同时按了Ctrl
cout<<"Left button down with CTRL pressed\n";
else
cout<<"Left button down\n";
}
else if(event==EVENT_LBUTTONUP) // 如果左键松开
cout<<"("<<x<<","<<y<<") Left button Up\n"; // 输出鼠标坐标
}
int main()
{
Mat im = imread("Flower.bmp");
if(im.empty()) return -1;
imshow("on_mouse", im);
// 注册回调:on_mouse窗口里鼠标动了,执行on_mouse函数
setMouseCallback("on_mouse", on_mouse);
while(waitKey(1)!=27) {} // 按Esc退出
}
-
-
类似的书上还有滑块事件的定义和注册P163,不过多介绍了
第十二章:PPT和CSDN上均无重点,估计不怎么考
纯数学概念,作为计算基础,本身不属于这门课的内容,也不会单独考
第十三章:图像变换
主要考傅立叶变化,理论基础太难,本科生无法战胜,这里只展示了代码部分的内容,想挑战理论部分的童鞋自行探索
傅立叶变化的核心代码过程就四步
载入灰度图片()调用imread函数
->转化为浮点类型(dft函数要求必须入参为浮点类型)
->傅立叶正交变化(dft函数)
->傅立叶逆变化(idft函数)
那么根据上述流程,核心代码就是如下
using namespace cv;
int main()
{
Mat X = imread("lena.jpg", 0); // 1. 载入灰度图像
Mat Y = (Mat1f)X; // 2. 转换为浮点型(Mat1f是浮点型矩阵的简写)
dft(Y, Y); // 3. 傅里叶正变换(核心)
idft(Y, Y, DFT_SCALE); // 4. 傅里叶逆变换(核心,DFT_SCALE是必要缩放)
}稍微加一点辅助代码,方便输出和对比
using namespace cv;
int main()
{
Mat X = imread("lena.jpg", 0); // 1. 载入灰度图像
Mat Y = (Mat1f)X; // 2. 转换为浮点型(Mat1f是浮点型矩阵的简写)
dft(Y, Y); // 3. 傅里叶正变换(核心)
idft(Y, Y, DFT_SCALE); // 4. 傅里叶逆变换(核心,DFT_SCALE是必要缩放)
Y = (Mat1b)Y; // 转换回uchar型方便显示(辅助步骤)
imshow("src", X); // 显示原图(辅助)
imshow("dst", Y); // 显示结果(辅助)
waitKey(); // 等待按键(辅助)
}书上P207的代码如下
using namespace cv;
int main()
{
// 载入灰度图像
Mat X = imread("lena.jpg", 0);
// 载入图像失败的判断
if (X.empty()) return -1;
// 显示源图像
imshow("源图像", X);
// 源图像转换为实数图像(适配傅里叶变换的格式要求)
X.convertTo(X, CV_32F);
// 傅里叶正变换,输出复数图像
dft(X, X, DFT_COMPLEX_OUTPUT);
int h = X.rows, w = X.cols; // 获取源图像的行数、列数
// 将靠近四角的元素改为0(与角部距离小于40)
for (int u = 0; u < w; ++u)
{
for (int v = 0; v < h; ++v)
{
// 计算相对最近角部的偏移量
int x = min(u, w - u), y = min(v, h - v);
// 行列号为(v,u)的位置,若距离角部过近则置0
if (x * x + y * y < 40 * 40) X.at<Vec2f>(v, u) = 0;
}
}
// 傅里叶逆变换,只存储实部(DFT_SCALE用于缩放结果)
idft(X, X, DFT_SCALE | DFT_REAL_OUTPUT);
// 增强高亮度和对比度(归一化处理)
normalize(X, X, 1, 0, NORM_INF);
// 显示结果图像
imshow("结果图像", X);
// 等待按键(防止窗口一闪而过)
waitKey();
}
第十四章:图像增强
图像平滑处理方法,参考P220中值滤波以及P222-223程序;图像的锐化,主要看拉普拉斯变换,程序题,本科生无法战胜理论
平滑处理方法
图像平滑处理的方法有三种:归一化块滤波器 ;高斯滤波器 ;中值滤波器,我们这里主要介绍中值滤波器的内容
中值滤波是一种非线性处理技术,可以用来抑制图像中的噪音,而且保持轮廓的清晰。
中值滤波使用当前像素旁的n(x) * n(y)个像素的灰度值的中值(中值不是平均值哈)作为当前像素的新的灰度值,即
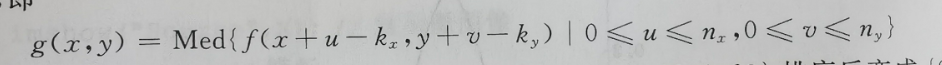
老规矩,聪明的大学生看不懂脑残的公式,直接上题解析

为了方便定位和解析,我们可以建立一下坐标系
| i\j-(i,j)表示某个数 | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 5 | 2 | 4 |
| 1 | 7 | 9 | 1 |
我们现在要做的就是利用中值,将所有的元素重新计算新值后覆盖即可
首先来看第一个元素,即(0,0)=5
我们以(0,0)这个元素为中心附近的3x3范围内的数据都写出来,然后求中值即可
(0,0)附近的元素(包含自己)有(-1,-1);(0,-1) ;(1,-1) ;(-1,0) ;(0,0) ;(1,0) ;(-1,1) ;(0,1) ;(1,1)
对应的上边坐标的数字,可以发现有一些负坐标的数据,肯定在表格中是不存在的,我们此时注意题意,边界外元素当边界元素处理,例如(-1,-1)最近的边界元素自然是(0,0),那么也就是5 ;(1,-1)最近的元素是(1,0)那么也就是7
y以此类推模板里的 9 个值(超出的部分用边界像素f(0,0)=5补):
f(-1,-1)=5(i=-1→0,j=-1→0)、f(-1,0)=5(i=-1→0)、f(-1,1)=2(i=-1→0)、
f(0,-1)=5(j=-1→0)、f(0,0)=5(原像素)、f(0,1)=2(原像素)、
f(1,-1)=7(j=-1→0)、f(1,0)=7(原像素)、f(1,1)=9(原像素)。
把这 9 个值排序:2,2,5,5,5,5,7,7,9,取第 5 个值→5,所以 g(0,0)=5。
同样的,将其余的几个都这样处理,分别得到新的数据,最后结果如下
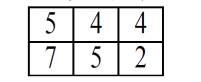
OpenCV中的平滑处理
OpenCV中提供了三个函数进行平滑处理
-
均值模糊:
void blur(InputArray src,OutputArray dst,Size ksize)-
src:输入图像 -
dst:输出图像 -
ksize:内核大小,必须为正奇数
-
-
中值模糊:
void medianBlur(InputArray src,OutputArray dst,int ksize)-
src:输入图像 -
dst:输出图像,大小和类型必须和源图像一致,必要时重建 -
ksize:内核大小,必须为正奇数
-
-
高斯模糊:
void GaussianBlur(InputArray src,OutputArray dst,Size ksize,double sigmaX,double sigmaY=0)-
src:输入图像 -
dst:输出图像,大小和类型必须和源图像一致,必要时重建 -
ksize:内核大小,必须为正奇数 -
sigmaX和sigmaY:高斯内核中的变量x和y的标准差
-
样例代码
// Smooth.cpp:OpenCV实现图像的三种平滑(模糊)处理
using namespace cv;
int main()
{
// 1. 读入灰度图像(路径是"lena-n.jpg",0表示以灰度模式读取)
Mat X = imread("lena-n.jpg", 0);
// 2. 判断图像是否读取失败(若失败则退出程序)
if (X.empty()) return -1;
// 3. 显示源图像
imshow("源图像", X);
Mat Y; // 用于存储每种模糊的结果图像
// --------------- 均值模糊 ---------------
blur(X, Y, {5,5}); // 参数:输入图像X、输出图像Y、模糊核大小5×5
imshow("简单模糊", Y);
// --------------- 中值模糊 ---------------
medianBlur(X, Y, 5); // 参数:输入图像X、输出图像Y、模糊核大小5(必须是奇数)
imshow("中值模糊", Y);
// --------------- 高斯模糊 ---------------
GaussianBlur(X, Y, {5,5}, 0, 0); // 参数:输入X、输出Y、核大小5×5、x/y方向标准差都是0
imshow("高斯模糊", Y);
// 等待按键(防止图像窗口一闪而过)
waitKey();
}
图像的锐化
常见的锐化方法包括Sobel算子的锐化,拉普拉斯算子的锐化和使用方向模板的锐化,这里我们主要介绍OpenCV中对于拉普拉斯算子的锐化的支持
核心方法:
-
void Laplacian(InputArray src,OutputArray dst,int ddepth)-
普通拉普拉斯变换,使用基本的拉普拉斯算子完成锐化,方法是对二阶x差分和y差分求和
-
第一个参数为输入图像;
-
第二个参数为输出图像,大小和通道数与源图像一致,必要时重建
-
第三个参数为目标图像的位深度,负数代表和源图像相同
-
-
void Laplacian(InputArray src,OutputArray dst,int ddepth,int size)-
拓展拉普拉斯变换,使用拓展的拉普拉斯算子完成锐化
-
第一个参数为输入图像;
-
第二个参数为输出图像,大小和通道数与源图像一致,必要时重建
-
第三个参数为目标图像的位深度,负数代表和源图像相同
-
第四个参数为内核大小,不超过31的奇数
-
// Laplace.cpp:OpenCV实现拉普拉斯锐化(增强图像边缘)
using namespace cv;
int main()
{
// 1. 读入灰度图像(路径为"lena.jpg",0表示灰度模式)
Mat X = imread("lena.jpg", 0);
// 2. 校验图像是否读取成功(失败则退出程序)
if (X.empty()) return -1;
// 3. 显示源图像(窗口名"Source")
imshow("Source", X);
// 4. 执行拉普拉斯锐化
// 参数说明:输入图像X、输出图像X、深度(-1表示与输入图像深度一致)、内核大小3×3
Laplacian(X, X, -1, 3);
// 5. 归一化处理(将结果亮度映射到0~255,方便观察锐化效果)
normalize(X, X, 255, 0, NORM_INF);
// 6. 显示拉普拉斯锐化后的结果
imshow("Laplace", X);
// 7. 等待按键(防止窗口一闪而过)
waitKey();
}
第十五章:图像解析
边缘检测,考程序,参考 P249的Canny边缘检测代码
using namespace cv;
int main()
{
// 1. 载入灰度图像(路径为"lena.jpg",0表示以灰度模式读取)
Mat X = imread("lena.jpg", 0);
// 2. 校验图像是否读取成功(失败则退出程序)
if (X.empty()) return -1;
// 3. 显示源图像(窗口名"Source")
imshow("Source", X);
Mat Y; // 存储Canny边缘检测的结果图像
// --------------- 第一次Canny检测(低阈值=28)---------------
// 参数说明:输入图像X、输出图像Y、低阈值=28、高阈值=3×28(Canny双阈值的常用比例:高阈值是低阈值的2~3倍)
Canny(X, Y, 28, 3*28);
// 显示该阈值下的边缘结果
imshow("Canny:28,3×28", Y);
// --------------- 第二次Canny检测(低阈值=68)---------------
// 参数:输入图像X、输出图像Y、低阈值=68、高阈值=3×68
Canny(X, Y, 68, 3*68);
// 显示该阈值下的边缘结果
imshow("Canny:68,3×68", Y);
// 4. 等待按键(防止图像窗口一闪而过)
waitKey();
}
猜题大王来猜题
第一章只讲了这两个点而且有一定的重复说明,疑似考试几率大
-
描述你对与计算机图形图像这么学科/技术的理解(论述题 or 简答题)
计算机图形图像学是一门融合数学、计算机科学、物理学与艺术设计的交叉学科,核心目标是用计算机实现图形图像的生成、处理、显示与交互,主要研究内容为图形的输入,图形的处理,图形的生成或输出,在工业,气象,医学,军事等多个方面均发挥着重要的作用 -
计算机图形图像和别的学科之间的关系(简答题)
计算机图形图形和图像处理,计算机视觉,计算几何这几门学科存在关联关系
计算机图形图像主要研究如何把数据模型转化为数字图像
图像处理主要研究数字图像的压缩存储和去噪等问题
计算机视觉主要研究如何把数字图像提取为数据和模型
计算几何主要研究数据模型的建立和存储
第六章
-
顶点变化的步骤
1:指定视图和造型变换,两者冲成为视图模型变换,将输入的顶点坐标转化为观察坐标
2:指定投影变换。该操作是投影变换和规范化变化的复合操作,将顶点从观察坐标变化为规范化坐标
3:指定视口变换,将规范化坐标转化为屏幕窗口坐标第八章
-
光源的构成
光源是由环境光成分,漫反射成分,镜面反射成分三个部分组成
文章标题:HNUST-计算机图形/图像期末复习-1.9 21:40更新
文章链接:https://zealsinger.xyz/?post=43
本站所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议,转载请注明来自ZealSinger !
如果觉得文章对您有用,请随意打赏。
您的支持是我们继续创作的动力!

微信扫一扫

支付宝扫一扫


(1)新增第二章内容,主要添加了帧缓冲器的定义和计算题,以及DDA画线算法
(2)进度到了所有的章节基本都有涉及了
(3)结合录音,ppt,题目进行了部分修改
(4)添加了“猜题大王模块”