«

开源项目HashSmith分享-一次PR经历-SwissTable和Robin Hood的学习

ZealSinger 发布于 阅读：1734 技术文档

摘要：

记录在reddit上看到一个UU发的贴子，发帖人bluuewhale提到了想写一个优于JDK底层的HashMap的Map，也就是本文要介绍的他所写的hash-smith: Fast & memory efficient hash tables for Java，在阅读他的这个项目的过程中，我尝试进行了Fork和PR，虽然只是一个很小的点，并且最终的因为需要权衡性能和内存最终暂且没有合并到主干，但是在这个过程中我也学到了该项目中提到的Hash算法和思路，以及和作者bluuewhale进行了长达两个2h的邮件交流，让我对于学习开源项目又有了新的体验和体会

知识背景

核心灵感：SwissTable和Robin Hood Hashing

SwissTable

简介

提到SwissTable，这个点其实不难，或者说没有想象的那么陌生，可能只是对于像我一样的纯粹的Javaer以及课外知识涉及不足的UU会觉得陌生一点（对知识贫瘠的无赖 ╮(╯_╰)╭ ）

SwissTable是Google推出的一种开放寻址的Hash方案，后来被整合到了Abseil，其核心优势在于分离元数据与数据存储以及低成本的探测，关键设计点是如下几个方面

当然，上述只是对于SwissTable设计的特点的简单描述，待会儿下文中我们会进行更加详细的过程介绍

SwissTable其实在提出以后，已经被很多语言的哈希表的底层设计认可，据网络资料获取到

从上述资料中可以知道，使用SwissTable无论实在Rust中还是Go语言中，带来的结果都是性能的大幅度提升，由此可见这个Hash方案的优秀之处。

Java为何没有实现

那么如此优秀的Hash方案，为何在Java中却迟迟没有实现和封装呢？我们不考虑历史包袱，那么主要原因是由于语言特性，技术依赖两个方面

破局思路

之前提到，Java中没有能让我们实现批处理这种向量计算支持的方式，但是在Java 16的时候，出现了Vector API用于专门支持向量计算，该项目一直处于孵化阶段，而在Java 24的时候已经算是接近稳定，Java 25进一步进行了优化（其实已经很完善了，但是据说JDK26依旧需要做第十一次孵化），故项目作者bluuewhale尝试基于Vector API实现符合Java的SwissTable，也就设计出了这个项目中的SwissMap 以及 SwissSimdMap

具体实现

我们来简单的来看一下SwissTable(SwissMap 以及 SwissSimdMap本质上的逻辑是差不多的，主要是硬件的适配i上的区别，所以我们不进行重复分析)

先来看看SwissMap中的定义的一些字段信息

private static final byte EMPTY = (byte) 0x80;    // 空槽位标记，标识槽位为空可以插入
private static final byte DELETED = (byte) 0xFE;  // 删除标记(墓碑)，标识槽位已被删除，作为墓碑标记
​
​
// 采用分组Hash，将一个元素的Hash分为高位和地位，高位确定所在group
private static final int H1_MASK = 0xFFFFFF80;  // 高位选择组
private static final int H2_MASK = 0x0000007F;  // 低位存储在控制字节中
​
​
private static final int GROUP_SIZE = 8;  // SWAR固定为一个组8个槽位(1个字)
​
​
// 默认负载因子为0.875，即当元素数量达到容量的87.5%时触发扩容
private static final double DEFAULT_LOAD_FACTOR = 0.875d;  // 类似Abseil SwissTable (7/8)
​
​
private static final long BITMASK_LSB = 0x0101010101010101L;  // 最低有效位掩码 用于广播单个字节到所有字节通道
private static final long BITMASK_MSB = 0x8080808080808080L;  // 最高有效位掩码，用于检测每个通道的最高位
​
​
​
private long[] ctrl;     // 每个long打包8个控制字节
private Object[] keys;   // 键存储
private Object[] vals;   // 值存储
private int tombstones;  // 已删除槽位数

然后我们看看SwissMap的初始化init()方法

@Override
// 入参为默认的大小 16
protected void init(int desiredCapacity) {
// 计算满足期望容量的最小组数
    int nGroups = Math.max(1, (desiredCapacity + GROUP_SIZE - 1) / GROUP_SIZE); 
    // 调整组数为大于等于原值的最小2次幂
    nGroups = ceilPow2(nGroups);
    // 组数*每组个数得到总容量
    this.capacity = nGroups * GROUP_SIZE;
// 相关数组的初始化
    this.ctrl = new long[nGroups];
    Arrays.fill(this.ctrl, broadcast(EMPTY));
    this.keys = new Object[capacity];
    this.vals = new Object[capacity];
    this.size = 0;
    this.tombstones = 0;
    // 根据负载因子和容量计算首次扩容阈值
    this.maxLoad = calcMaxLoad(this.capacity);
}
​

然后我们来看看对应的put()方法。先不管reHash的过程

@Override
public V put(K key, V value) {
    // 是否需要ReHash
    maybeRehash();
    return putVal(key, value);
}
​
​
private V putVal(K key, V value) {
    // 计算key对应的h1和h2两个hash值，确定组和指纹
        int h = hash(key);
        int h1 = h1(h);
        byte h2 = h2(h);
        int nGroups = numGroups();
        int mask = nGroups - 1; // 组索引掩码（替代取模，优化性能）
        int firstTombstone = -1;  // 记录遍历中遇到的第一个墓碑位置（优先复用）
        int visitedGroups = 0;  // 已经遍历的组数 防止死循环
        int g = h1 & mask; // optimized modulo operation (same as h1 % nGroups)  得到初始组索引
        for (;;) {
            int base = g * GROUP_SIZE;  // 当前组的槽位基索引（组内第一个槽位的全局索引）
            long word = loadCtrlWord(g); //  加载当前组的控制字段 ctrl[group]  一个组的size=8位 刚好就是一个long类型 打包成一个long类型是批处理的关键
            // 下面属于组内匹配过程 查找是否已经存在该key
            long eqMask = eqMask(word, h2);  // 生成掩码：组内控制字节=h2的槽位，对应位设为1
            while (eqMask != 0) {  // 遍历h2相匹配的槽位
                int idx = base + nextEmptySlotIndex(eqMask);  // 找到掩码中最低位的1 → 对应槽位索引，也就是找到匹配h2最近的那个槽位
                if (Objects.equals(keys[idx], key)) {  // 比较指纹 如果key相同则覆盖且返回旧的value
                    V old = (V) vals[idx];
                    vals[idx] = value;
                    return old;
                }
                eqMask &= eqMask - 1; // clear LSB 经典位运算，清除最低位的 1（比如 0b1010 → 0b1000），保证能匹配到下一位，从而实现遍历所有匹配槽位
            }
            // 记录第一个墓碑的位置 
            if (firstTombstone < 0) { 
                long delMask = eqMask(word, DELETED);// 生成掩码：组内控制字节=DELETED的槽位
                if (delMask != 0) firstTombstone = base + nextEmptySlotIndex(delMask); // 依旧是筛选出第一个墓碑槽位
            }
            // 找到下一个空位 
            long emptyMask = eqMask(word, EMPTY);
            if (emptyMask != 0) {
                int idx = base + nextEmptySlotIndex(emptyMask);
                int target = (firstTombstone >= 0) ? firstTombstone : idx; // 优先复用墓碑 如果没有墓碑再使用第一个空位
                return insertAt(target, key, value, h2); // 插入数据 对应的key/value数组的target位置放入数据，并且更新ctrl[target]数组中对应的位置从DELETED/EMPTY修改为h2
            }
            if (++visitedGroups >= nGroups) { // 递增已经遍历的组的数量 当所有的组数量遍历完了无空槽。实际上这个地方大概率不会触发，因为会有扩容操作的存在，不会出现无空槽的情况，属于防御性编程
                throw new IllegalStateException("Probe cycle exhausted; table appears full of tombstones");
            }
            g = (g + 1) & mask; // 组索引增加，外层for循环就是在遍历所有的组，查找所有的组，只不过是从h1计算得到的索引位置开始遍历
        }
    }

其中比较重要的两个方法就是eqMask(long word, byte b)和nextEmptySlotIndex(long mask),我们可以来分析一下

eqMask

这个 eqMask 方法是 SwissMap 中 SWAR（单指令多数据）批量字节匹配 的核心实现，目标是：接收一个 8 字节的控制字（word，对应 8 个槽位的控制字节）和一个目标字节 b，返回一个 8 位掩码（long 类型，但仅低 8 位有效）—— 掩码的第 i 位为 1，表示控制字中第 i 个字节等于 b；为 0 则不等。

整个过程利用两个前置常量BITMASK_LSB 和 BITMASK_MSB，以及broadcast()方法

private long eqMask(long word, byte b) {
    long x = word ^ broadcast(b);
    long m = (x - BITMASK_LSB) & ~x & BITMASK_MSB;
    return m >>> 7;
}
​
private long broadcast(byte b) {
    // Broadcast a single byte to all 8 byte lanes
    return toUnsignedByte(b) * BITMASK_LSB;
}
​
​
private static long toUnsignedByte(byte b) {
    // Unsigned widening to avoid sign extension on negative bytes
    return b & 0xFFL;
}

broadcast方法的作用就是将字节b转化为八进制，然后利用异或（^）特性：两个二进制位相同则为 0，不同则为1，则可以将得到x，x中是每一位上，word和b不一致的就会标记非0，相同则标记为0（0X00）

假设控制字 word = 0x0201020102010000L（8 个字节：00,00,01,02,01,02,01,02），
目标字节 b = 0x02；broadcast(b) = 0x0202020202020202L；
异或后 x = 0x0001000100010202L（字节级：02^02=00, 01^02=01, 02^02=00, 01^02=01, 02^02=00, 01^02=01, 00^02=02, 00^02=02）。

然后经过(x - BITMASK_LSB) & ~x & BITMASK_MSB提取 “匹配字节” 的标记位

子步骤 2.1：x - BITMASK_LSB —— 利用下溢标记 0 字节
BITMASK_LSB = 0x0101010101010101L，对 x 每个字节位独立减 1：
若 x 的第 i 个字节是 0x00 → 减 1 后下溢（0-1=-1），该字节变为 0xFF（二进制 11111111），其最高位（第 7 位）为 1；
若 x 的第 i 个字节非 0 → 减 1 后最高位仍为 0（如 0x01-1=0x00、0x02-1=0x01，最高位都是 0）。
示例续：x = 0x0001000100010202L - 0x0101010101010101L = 0xFF00FF00FF000101L；（字节级：00-01=FF, 01-01=00, 00-01=FF, 01-01=00, 00-01=FF, 01-01=00, 02-01=01, 02-01=01）。
​
​
子步骤 2.2：& ~x —— 过滤非 0 字节的干扰
~x 是 x 的按位取反（字节级取反）：
若 x 的第 i 个字节是 0x00 → ~x 该字节为 0xFF → 与运算后保留子步骤 2.1 的结果；
若 x 的第 i 个字节非 0 → ~x 该字节非 0xFF → 与运算后清除子步骤 2.1 中可能的无效位。
示例续：~x = 0xFFFEFFFEFFFEFDFDL；0xFF00FF00FF000101L & 0xFFFEFFFEFFFEFDFDL = 0xFF00FF00FF000000L；（仅保留 x 中 0 字节对应的下溢位，其余清零）。
​
​
子步骤 2.3：& BITMASK_MSB —— 仅保留最高位标记
BITMASK_MSB = 0x8080808080808080L，作用是只保留每个字节的最高位，其余位清 0 —— 最终 m 中，只有 x 里值为 0 的字节（匹配 b 的字节），其最高位为 1，其余为 0。
示例续：0xFF00FF00FF000000L & 0x8080808080808080L = 0x8000800080000000L；（仅保留 3 个匹配字节的最高位 1，其余为 0）。

最后将m右移七位，把 8 字节的标记（m）压缩为 8 位掩码（long 的低 8 位），掩码的第 i 位对应控制字的第 i 个字节是否匹配 b

右移 7 位的唯一目的，是把这些标记挪到 8 的倍数位，方便进行高效的运算

m = 0x8000800080000000L >>> 7 = 0x0100010001000000L；
二进制串（左→右）：00000001 00000000 00000001 00000000 00000001 00000000 00000000 00000000
对应全局位索引：   63~56     55~48     47~40     39~32     31~24     23~16     15~8      7~0
每8位一个槽位 右移之后为3，5，7，那么原来的就是2，4，6槽位
nextEmptySlotIndex

然后是nextEmptySlotIndex()方法

private int nextEmptySlotIndex(long mask) {
    return (int) (Long.numberOfTrailingZeros(mask) >>> 3);
}

这个 nextEmptySlotIndex 方法是 SwissMap 中 “8 位间隔掩码”→“组内槽位索引” 的核心转换工具，专门适配 eqMask 返回的掩码格式，最终输出组内 0~7 的槽位索引（因为 SwissMap 每个 Group 固定 8 个槽位）

用上面的0x0100010001000000L放到方法中测试一下

十六进制：0x0100010001000000L
64位二进制（左→右对应全局位63~0）：
00000001 00000000 00000001 00000000 00000001 00000000 00000000 00000000
全局位索引范围：63~56   55~48   47~40   39~32   31~24   23~16   15~8    7~0
​
numberOfTrailingZeros查找最低位开始最长连续的0的个数（也可以理解找最低位的1）那么也就是24位
>>>3 其实就是除以 2^3 也就是除以8  那么得的就是3，也就对应3号槽位，和上面eqMask方法对应的上
实际存储

说了这么多理论，我们可以从宏观角度来看看整个数据的存储如何进行的

我们定义两个测试键：

步骤 1：初始化

控制字节数组全为 EMPTY(0x00)，键 / 值数组为空：

索引 0 1 2 3 4 5 6 ... 15
Control 00 00 00 00 00 00 00 ... 00
Keys - - - - - - - ... -
Values - - - - - - - ... -

步骤 2：插入 KeyA（值 = 10）

  1. 计算理想位置 = 4，读取控制字节 [4] → EMPTY；

  2. 将 Control [4] 标记为 OCCUPIED(0x01)；

  3. Keys[4] = KeyA，Values[4] = 10；

此时状态：

索引 4 5 6
Control 01 00 00
Keys A - -
Values 10 - -

步骤 3：插入 KeyB（值 = 20，哈希冲突）

  1. 计算理想位置 = 4，读取 Control [4] → OCCUPIED（冲突）；

  2. SWAR 批量探测：一次读取 Control [4~11]（8 个字节），快速过滤出第一个 EMPTY 槽位（索引 5）；这个读取过程也符合我们之前分析代码，从理想位置的索引位置开始往后遍历所有的槽

  3. 将 Control [5] 标记为 OCCUPIED(0x01)；

  4. Keys[5] = KeyB，Values[5] = 20；

此时状态：

索引 4 5 6
Control 01 01 00
Keys A B -
Values 10 20 -

步骤 4：查询 KeyB

  1. 计算理想位置 = 4，通过 SWAR 批量读取 Control [4~11]，快速筛选出所有 OCCUPIED 槽位（索引 4、5）；

  2. 仅对比这两个槽位的键：Keys [4]=A（不匹配）→ Keys [5]=B（匹配）；

  3. 返回 Values [5]=20；

对比 HashMap：无需遍历链表，批量过滤后仅需对比少量候选槽位，效率更高。

步骤 5：删除 KeyA（触发墓碑机制）

SwissMap 不直接清空槽位，而是标记「墓碑」，这是其核心设计：

  1. 定位 KeyA 所在索引 4，将 Control [4] 从 OCCUPIED(01) 改为 TOMBSTONE(02)；

  2. 保留 Keys [4] 和 Values [4]（可置空，不影响，核心是控制字节标记）；

此时状态（关键：索引 4 是墓碑）：

索引 4 5 6
Control 02 01 00
Keys A B -
Values 10 20 -

步骤 6：复用墓碑（插入 KeyD，值 = 40，hash=100）

墓碑的核心价值是「复用空位，避免探测链断裂」：

  1. 计算理想位置 = 4，读取 Control [4] → TOMBSTONE（可复用）；

  2. 将 Control [4] 从 TOMBSTONE(02) 改回 OCCUPIED(01)；

  3. 覆盖 Keys [4]=D，Values [4]=40；

此时状态（墓碑被复用）：

索引 4 5 6
Control 01 01 00
Keys D B -
Values 40 20 -

SwissTable实际上就是开发地址法，开放地址法的致命问题是「删除槽位会断裂探测链」：

  • 若直接清空索引 4（设为 EMPTY），查询 KeyB 时，会导致先查到这个empty所在index，从而导致equal中无法相等，然后直接跳过当前槽；（具体可以看源码中的findValue方法）

  • 标记为墓碑后，查询时会跳过墓碑继续探测，插入时可复用墓碑，既保证探测链连续，又避免空位浪费。

RobinHoodMap

除了上述的SwissMap，作者还实现了一个采用 Robin Hood 哈希，冲突时通过「移动元素」平衡探测距离（元素的探测距离越接近其理想位置越好），避免长探测链。

从Robin Hood Hashing 源码分析 | SF-Zhou's Blog了解到，C++ 13中的robin_hood::unordered_map就是传统std::unordered_map的替代品，性能提高了2-3倍

因为不是本次的重点，所以这个Hash方式我们简单的用实际操作，不去分析源码设计了。

RobinHood 哈希中需要弄明白如下公式以及公式中变量的关系：探测距离 = (实际位置 - 理想位置) % 哈希表容量

RobinHood 哈希的核心逻辑是 “劫富济贫” 式的位置交换 ：当插入新元素时，若遇到一个 “探测距离比自己大” 的已存元素（更委屈的元素），就交换两者的位置 —— 最终让这个 “委屈” 的元素（大探测距离）向它自己的理想位置靠近，而非向 “别人的理想位置” 靠近。

我们设定：

二、先看「普通线性探测」的插入（暴露问题）

普通线性探测的逻辑：理想位置被占，就一直往后找空位置，不交换任何元素，最终导致后插入的元素被 “挤到远处”。

插入步骤 操作 实际位置 探测距离 d 哈希表状态（索引 0-7）
1. 插入 KeyA 理想位置 4 为空，直接放入 4 0 [空，空，空，空，A, 空，空，空]
2. 插入 KeyB 理想位置 4 被占，探测 5（空），放入 5 1 [空，空，空，空，A,B, 空，空]
3. 插入 KeyC 理想位置 4、5 被占，探测 6（空），放入 6 2 [空，空，空，空，A,B,C, 空]
4. 插入 KeyD 理想位置 4、5、6 被占，探测 7（空），放入 7 3 [空，空，空，空，A,B,C,D]

普通线性探测的问题：

三、再看「RobinHood 哈希」的插入（核心是 “交换 + 劫富济贫”）

RobinHood 的核心规则：

  1. 插入新元素时，先按线性探测找空位置，计算自己的探测距离 d_new；

  2. 若探测路径上遇到已存在的元素，计算其探测距离 d_old；

  3. 若 d_new > d_old

    （已存元素更 “委屈”），则交换两者位置

    • 原已存元素（更委屈）移动到新元素的当前探测位置（离自己的理想位置更近，d 变小）；

    • 新元素接管原已存元素的位置，继续往后探测；

  4. 重复步骤 2-3，直到找到空位置插入。

分步拆解 RobinHood 插入 KeyA→KeyB→KeyC→KeyD 的全过程

所有 Key 的理想位置均为 4，按顺序插入，每一步都标注「探测位置、d 计算、是否交换、最终状态」。

步骤 1：插入 KeyA（无冲突，无交换）

  1. 计算 KeyA 的理想位置：4；

  2. 探测位置 4：为空，直接放入；

  3. 计算 KeyA 的 d：d = 4 - 4 = 0（无委屈，在自己理想位置）；

  4. 哈希表状态（索引 0~7）：[空, 空, 空, 空, A, 空, 空, 空]。

步骤 2：插入 KeyB（无冲突，无交换）

  1. 计算 KeyB 的理想位置：4；

  2. 探测位置 4：被 KeyA 占据，继续探测下一个位置 5；

  3. 探测位置 5：为空，计算 KeyB 若放入 5 的 d_new：d_new = 5 - 4 = 1；

  4. 位置 5 无已存元素，直接放入；

  5. 计算 KeyB 的 d：d = 1；

  6. 哈希表状态：[空, 空, 空, 空, A, B, 空, 空]。

步骤 3：插入 KeyC（无交换，仅线性探测）

  1. 计算 KeyC 的理想位置：4；

  2. 探测位置 4：被 A 占据（A 的 d_old=0），KeyC 若放 4 的 d_new=0 → d_new（0）=d_old（0）→ 不交换，继续探测位置 5；

  3. 探测位置 5：被 B 占据（B 的 d_old=1），KeyC 若放 5 的 d_new=1 → d_new（1）=d_old（1）→ 不交换，继续探测位置 6；

  4. 探测位置 6：为空，计算 KeyC 若放入 6 的 d_new：d_new = 6 - 4 = 2；

  5. 位置 6 无已存元素，直接放入；

  6. 计算 KeyC 的 d：d = 2；

  7. 哈希表状态：[空, 空, 空, 空, A, B, C, 空]。

步骤 4：插入 KeyD（核心交换场景，重点！）

这是体现 RobinHood 核心逻辑的关键步骤，逐阶段拆解探测和交换过程：

  1. 计算 KeyD 的理想位置：4；

  2. 阶段 1：探测位置 4（被 A 占据）

    • KeyD 若放 4 的 d_new：4-4=0；

    • 已存元素 A 的 d_old=0 → d_new（0）=d_old（0）→ 不交换，继续探测位置 5；

  3. 阶段 2：探测位置 5（被 B 占据）

    • KeyD 若放 5 的 d_new：5-4=1；

    • 已存元素 B 的 d_old=1 → d_new（1）=d_old（1）→ 不交换，继续探测位置 6；

  4. 阶段 3：探测位置 6（被 C 占据）

    • KeyD 若放 6 的 d_new：6-4=2；

    • 已存元素 C 的 d_old=2 → d_new（2）=d_old（2）→ 不交换，继续探测位置 7；

  5. 阶段 4：探测位置 7（为空，触发交换判断）

    • KeyD 若放 7 的 d_new：7-4=3；

    • 此时回头看 “最后一个被占据的位置 6（C）”：C 的 d_old=2；

    • 对比：d_new（3）> d_old（2）→ 满足交换规则（KeyD 更委屈），触发交换；

  6. 阶段 5：执行交换（KeyC ↔ KeyD）

    • 交换逻辑：KeyD（更委屈）有权占据离理想位置更近的 6 号位，KeyC 替 KeyD 承担 7 号位；

    • 交换后：

      KeyD 移到 6 号位，d=6-4=2（从原本的 3→2，离理想位置 4 更近）；

      KeyC 移到 7 号位，d=7-4=3（从原本的 2→3，替 D 承担委屈）；

  7. 最终状态

    • KeyD 的实际位置：6，d=2；

    • KeyC 的实际位置：7，d=3；

    • 哈希表状态：[空, 空, 空, 空, A, B, D, C]。

三、插入完成后：核心数据对比（体现 RobinHood 的价值）

元素 实际位置 探测距离 d 离理想位置 4 的距离 核心变化（对比 “不交换的普通线性探测”）
A 4 0 0（最近） 无变化
B 5 1 1 无变化
D 6 2 2 普通探测中 D 会在 7 号位（d=3），交换后 d=2，离理想位置更近
C 7 3 3（最远） 普通探测中 C 会在 6 号位（d=2），交换后替 D 承担更大的 d

更加详细的可以看C++ 浅谈Robin Hood Hash 算法

PR过程

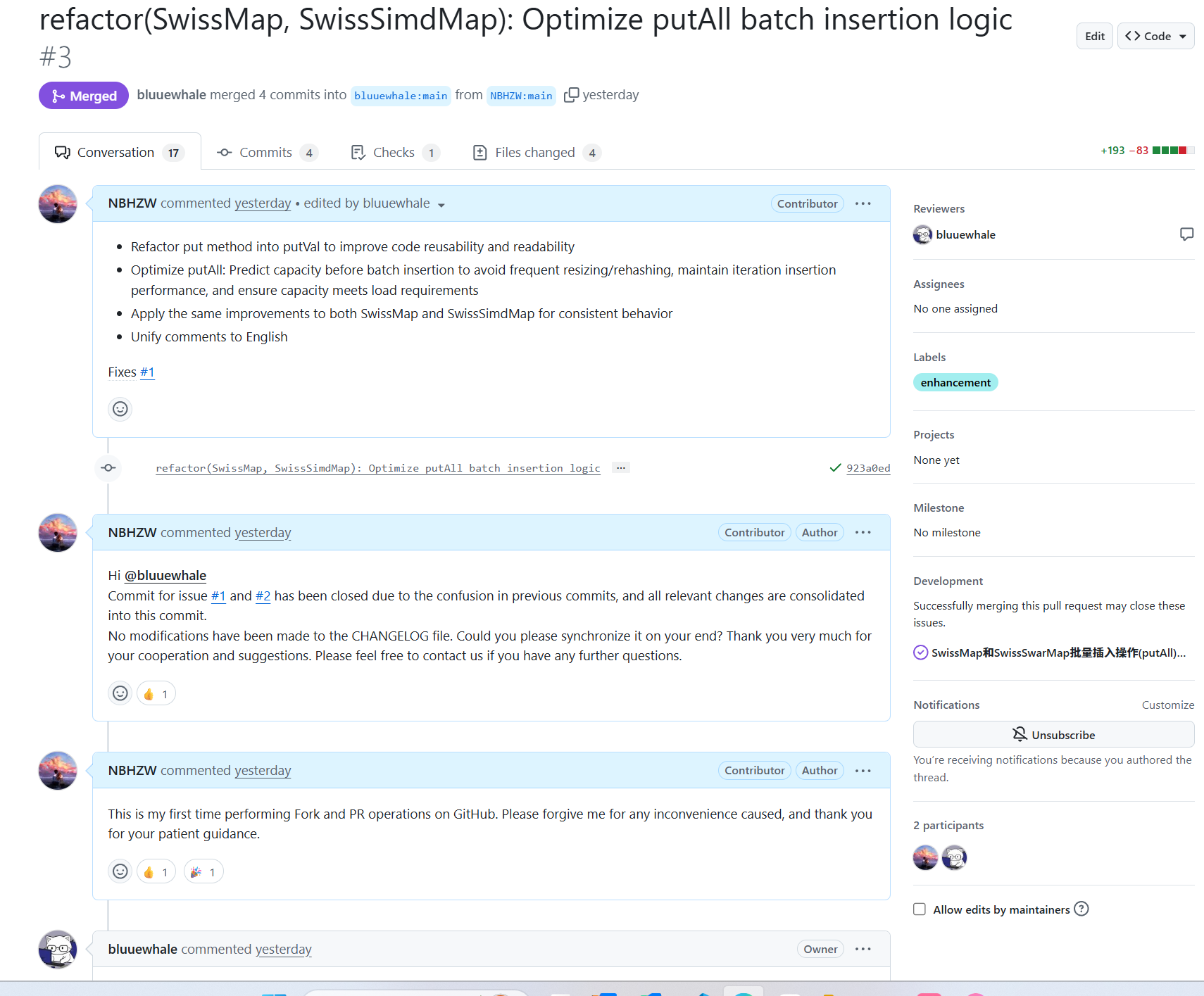
整个PR过程其实比较简陋，其实就是修改了SwissMap的putAll方法，整个putAll方法中原本的逻辑是直接循环调用put方法，很明显啊，这个过程可能会导致put中的ReHash循环的被执行，从而导致过于频繁的扩容。

为了提高效率，我将其修改为先通过size预估出要扩容的大小，先进行整体的扩容然后再执行放入，这样就能很好的防止频繁的扩容操作。

但是其实这里也出现了另外一个问题，如果批量新增的这个map和已经存在map中重复数据比较多，就会导致无意义的额外扩容，这个其实在JDK 的 HashMap的putAll方法的源码中一样存在这种问题。这个其实就是一个时间和空间之间的取舍问题。

经过和作者交流，虽然我们两最后还是没有拍板确认最终方案，但是讨论出了更加合理的扩容阈值计算，以及对于后续的探讨确认。

image-20251215232519865

编程 Java 项目

文章作者：ZealSinger
文章标题：开源项目HashSmith分享-一次PR经历-SwissTable和Robin Hood的学习
文章链接：https://zealsinger.xyz/?post=46
本站所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议，转载请注明来自ZealSinger ！

📚 推荐阅读